Машинное деление целых двоичных чисел
17.01.2019
Эта статья размещена в разделе практики программирования, а не в разделе для начинающих, что было бы логичнее, на первый взгляд. Но вопросы по делению, и умножению, как не странно, не редко встречаются и на серьезных форумах, причем далеко не только от новичков.
В статье Простые типы данных. Машинное представление простых типов. Операции с простыми типами. я написал об арифметических операциях над машинными типами данных, но "оставил за кадром" их программную реализацию в случае отсутствия соответствующей команды у процессора. Безусловно, сложение и вычитание есть в наборе команд всех процессоров. Обычно есть и, как минимум, некоторые типы сдвигов. Сложнее обстоит дело с умножением и делением. Даже не все "настоящие" ЭВМ имели такие команды в своем наборе инструкций. Дело в сложности аппаратной реализации. Обычные логические операции реализуются дискретной логикой легко. Со сдвигами (по крайней мере на один разряд) тоже не возникает особых сложностей. Сложение и вычитание уже сложнее и требуют большего количества логических элементов. А умножение и деление требуют или циклического выполнения нескольких более простых операций, или очень громоздких схем. В современных микропроцессорах, где реализованы почти все возможные операции, умножение и деление, обычно, реализованы на микропрограммном уровне и медленнее логических операций и сложения с вычитанием. Что уж говорить о микроконтроллерах, где эти операции встречаются далеко не во всех моделях. С умножением чуть проще, эта команда встречается у гораздо большего количества контроллеров. А вот делению повезло меньше, так как эта операция сложнее. При этом умножать и делить иногда все таки бывает нужно. Давайте отбросим советы "сменить контроллер", это не всегда возможно, и посмотрим, что можно сделать. В этой статье поговорим о делении целых беззнаковых чисел. Для иллюстрации я выбрал линейку 8-битных микроконтроллеров MidRange PIC компании Microchip, но все описанное применимо и к другим, например для ATtiny10 и ATtiny13 архитектуры AVR (хотя программы, разумеется, будут другими).
Сначала напомню, что деление на степени двойки можно заменить сдвигом делимого вправо. Например, деление на 8 равнозначно сдвигу на три разряда вправо. При этом мы можем сохранять выдвигаемые разряды в отдельной переменной, которая будет являться остатком от деления. Если у нас делитель известен на этапе написания программы мы можем сразу заменить деление на комбинацию сдвигов, вычитаний и сложений. Зачастую это будет выполняться быстрее собственно деления. Сложности начинаются тогда, когда у нас делитель становится известен только на этапе выполнения. Тут уже нужно какое то универсальное решение.
Существующие алгоритмы деления, в большинстве своем, так или иначе сводятся к привычному всем делению столбиком. Для тех, кто давно ничего не считал вручную, напомню, как это выглядит
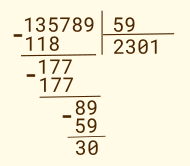
Частное от деления равно 2301, а остаток 30. Обратите внимание, что результатом являются два числа, а не одно, как в стандартных операциях языков высокого уровня, например, С. Это бывает важно, например, при преобразованиях систем счисления (для вывода на индикатор числа в десятичном виде, например). В программе на языке С нам бы пришлось для получения частного использовать операцию "/", а для получения остатка операцию "%" (или умножение с вычитанием, что не проще). При том, что достаточно только деления. Да, проблема решается библиотечными процедурами, но они не всегда доступны, например, могут отсутствовать в бесплатной версии компилятора. Наша реализация деления позволит получать оба числа за одну операцию (за один вызов процедуры). Так что это полезно не только тем, кто пишет программы на ассемблере.
Уже сейчас можно заметить основные принципы деления столбиком. Во первых, мы начинаем со старших, самых левых, цифр делимого и двигаемся вправо, к младшим цифрам. Если очередной остаток от вычитания с очередной "снесенной" цифрой делимого меньше делителя, то в результат заносится 0 и "сносится" очередная цифра делимого. Причем частное у нас начинает получаться начиная с самой старшей, самой левой цифры. С двоичными числами все будет проще.
Деление 8 разрядных беззнаковых чисел
Поскольку наиболее просто и наглядно деление реализуется для естественной для процессора разрядности или меньшей, а у нас 8-битный контроллер, то начнем с деления 8-битного числа на 8-битное. Знак частного и остатка легко учесть отдельно, если это требуется. Для примера разделим 185 на 17. В шестнадцатиричном виде это будет деление B9 на 11. А в двоичном 10111001 на 00010001. Вот как это будет выглядеть "в столбик"
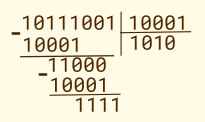
Частное 10 и остаток 15. Пример получился довольно коротким. Но сам принцип и основные шаги видно. И они такие же, как для десятичного деления. А вот дальше я вас немного запутаю (но потом, обязательно, распутаю). Для начала вспомним, что в этом мире все относительно и еще раз посмотрим на примеры деления. Да, делитель сдвигается вправо относительно делимого в процессе деления. Но ведь можно сказать, что делимое сдвигается влево относительно делителя. Казалось бы, какая разница? На результат это не должно влиять. Забегая вперед могу сказать, что действительно не влияет. Результат деления будет одинаков. Ну почти одинаков. Но дьявол, как известно, кроется в деталях. И это детали реализации, причем довольно важные.Давайте разбираться.
Алгоритм деления, вариант первый, сдвигаем делитель
Сначала попробуем написать алгоритм "в лоб", как обычно делят в столбик. То есть, делимое оставим на месте, а будем двигать вправо делитель.
Проверка делителя на ноль. Для этого варианта алгоритма важный шаг. Иначе программа зациклится на следующем шаге. Да и школьные правила деления говорят, что на ноль делить нельзя.
Нормализация. Именно так этот шаг алгоритма обычно называют. Дело в том, что начинать мы должны с самого старшего разряда. А это означает, что самый старший разряд делителя должен быть равным 1. Что бы достичь этого мы сдвигаем делитель влево столько раз, сколько потребуется. Но не забываем считать, сколько сдвигов сделали. Число разрядов частного будет равно числу сдвигов плюс 1. Плюс 1, так как как минимум одно вычитание (один разряд частного) будет даже при отсутствии необходимости сдвигать делитель.
Вычитание и определение значения очередного разряда частного. Вычитаем сдвинутый делитель из делимого. Если разность положительна, то есть, делимое больше делителя, то в частное вдвигаем справа единицу. При этом разность становится новым значением делимого. Если разность отрицательна, то вдвигаем в частное ноль, а делимое оставляем без изменений.
Сдвиг делителя. Сдвигаем делитель на один разряд вправо.
Проверка завершения деления. Уменьшаем на 1 счетчик вычитаний (его мы получили на первом шаге). Если он стал 0, то деление закончено. При этом делимое будет равно остатку. Если же счетчик не равен 0, то возвращаемся к шагу 3.
Вот так все просто. Нам не надо пытаться угадать, или подобрать, очередную цифру частного, что значительно усложняет алгоритмы десятичного деления. При этом цикл деления у нас будет переменной длины. Своего рода оптимизация.
Прежде, чем переходить к тексту программы нужно сказать буквально пару слов об архитектуре и системе команд MidRange PIC, что бы те, кто незнаком с этими микроконтроллерами появилась возможность уловить суть. Более подробно о системе команд MidRange PIC вы можете прочитать здесь. А особенности конкретной модели, которую собираетесь использовать, нужно искать в документации производителя.
В микроконтроллерах MidRange PIC память данных представлена виде "регистровых файлов" (терминология Microchip) разделенных на банки. При этом каждый такой регистр, или ячейка памяти данных, может быть напрямую адресована в коде команды. Углубляться в тонкости организации и управления банками памяти данных не буду, нам это почти не потребуется. В PIC нет двухадресных команд. Там, где команде требуется два операнда, неявно используется специальный рабочий регистр W (WREG), что, впрочем, часто отражается в мнемонике команды. Результат выполнения команды может, за некоторым исключением, помещаться обратно в адресуемую командой ячейку памяти или в WREG. Флаг переноса С размещен в регистре STATUS и для команды вычитания имеет инверсное значение. То есть, 1 состояние флага свидетельствует об отсутствии переноса (положительная разность), а 0 наличию переноса (отрицательная разность). При этом на флаг переноса влияет ограниченное количество команд. Команды проверки нулевого значения или знака регистра или ячейки памяти нет, но флаг Z существует. Есть и экзотические команды проверки бита и пропуска следующей команды по условию, они заменяют команды условных переходов. И удобные, но трудно воспринимаемые новичками, команды инкремента декремента с одновременной проверкой на нулевой результат, которые часто применяют для организации циклов.
А теперь, наконец, текст программы деления. Специально несколько излишне прокомментировал каждый шаг, для тех, кто не знаком с микроконтроллером.
;
; Секция данных процедуры деления.
;
div_dat udata_shr
dividend res 1 ; делимое, один байт
divider res 1 ; делитель, один байт
quotient res 1 ; частное, один байт
remainder res 1 ; остаток, один байт
counter res 1 ; счетчик сдвигов/вычитаний
;
; Секция кода процедуры деления.
;
Division code
Udiv8x8:
; Шаг 1, проверка делителя
movf divider,f ; Проверяем равенство делителя нулю
btfsc STATUS,Z
goto Overflow ; На ноль делить нельзя
; Начальная инициализация переменных
clrf quotient ; Необходимо, так как может быть
; меньше 8 сдвигов
movlw 1
movwf counter
; Шаг 2, нормализация
Step2:
btfsc divider,7 ; Проверяем старший бит делителя
goto Step3 ; 1, переходим к шагу 3
bcf STATUS,C ; Сбрасываем флаг переноса
rlf divider,f ; Сдвигаем делитель влево
incf counter,f ; Увеличиваем счетчик сдвигов
goto Step2 ; Продолжаем нормализацию
; Шаг 3, выполняем вычитание и определяем очередной разряд частного
Step3:
movf divider,w ; Загружаем делитель в WREG
subwf dividend,w ; Вычитаем делитель из делимого
; разность помещаем в WREG
btfss STATUS,C ; Проверяем знак разности
goto S3Neg ; Разность отрицательна
rlf quotient,f ; Положительна, помещаем 1
; в очередной разряд частного
movwf dividend ; Помещаем разность на место делимого
goto Step4
S3Neg:
rlf quotient,f ; Помещаем 0 в очередной разряд частного
; шаг 4, сдвиг делителя
Step4:
rrf divider,f ; Сдвиг делителя вправо на 1 разряд
; Шаг 5, проверка завершения
decfsz counter,f ; Уменьшаем счетчик
goto Step3 ; Не 0, продолжаем
movf dividend,w ; Копируем остаток на место результата
movwf remainder
bcf STATUS,C
return
Overflow:
bsf STATUS,C ; Для индикации ошибки устанавливаем
; флаг переноса
return ; И завершаем работу
В начале программы размещены используемые параметры и рабочие переменные. Что бы не возиться с банками памяти они размещены в разделяемой между всеми банками области. Такое есть в некоторых моделях. Сама процедура размещается в секции Division и называется Udiv8x8. Процедура полностью рабочая и занимает в памяти программ 29 слов (по 14 разрядов, такова организация памяти программ). Кроме того, использовано 5 байт в памяти данных.
Давайте попробуем оценить быстродействие, то есть, количество машинных циклов для выполнения деления. Почти все команды, за исключением команд передачи управления, которым нужно два цикла, выполняются за один машинный цикл. Команды btfsc и btfss выполняются за один или два цикла, в зависимости от значения проверяемого бита. Команда decfsz выполняется за один или два цикла, в зависимости от равенства нулю своего операнда после выполнения декремента. При этом будем считать, что делитель не равен нулю, так иначе нам не интересен результат.
Поскольку у нас количество итераций цикла переменное, то точное быстродействие подсчитать не просто. Проверка делителя займет 3 машинных цикла. Нормализация может выполняться от 3, когда старший бит делителя равен единице, до 52 циклов, когда делитель равен 1. Первый шаг и начальная инициализация переменных выполнятся за 5 циклов в любом случае. Остальные шаги выполнятся за 9 или 11 циклов на каждую итерацию цикла. Например, для нашего примера деления 185 на 17 потребуется 4 итерации. И завершающая часть программы, вместе с инструкцией возврата, потребует 5 циклов. Получается, что в лучшем случае потребуется примерно 25 машинных циклов, а в худшем примерно 137. Не очень быстро. И занимает довольно много места в памяти программ. Чем больше в делителе значащих разрядов, тем быстрее выполняется деление.
Алгоритм деления, вариант второй, сдвигаем делимое
А теперь попробуем пойти по менее очевидному пути, сдвигать не делитель, а делимое. Причем всегда будем выполнять 8 итераций цикла, по одной на каждый бит. При этом у нас автоматически получится обработка начиная со старших разрядов, а остаток будет сразу формироваться на нужном месте, как и частное. Да еще и проверка делителя на нулевое значение не потребуется, так как это не приведет к неработоспособности алгоритма
Устанавливаем значение счетчика циклов равное количеству разрядов делимого, то есть 8, в нашем случае.
Сдвигаем содержимое делимого влево, вдвигая выдвигаемый старший разряд в остаток.
Вычитаем делитель из остатка. Фактически, это вычитание из старших разрядов делимого, которые мы постепенно перемещаем на место остатка. Как и в первом варианте алгоритма, если разность положительна, то мы вдвигаем в частное слева единицу, а разность помещаем на место остатка, замещая таким образом обработанные разряды делимого. Если разность отрицательна, то в частное слева вдвигаем ноль, а значение остатка оставляем без изменений.
Уменьшаем на единицу счетчик итераций цикла. Если он стал равен нулю, деление закончено. При этом и остаток, и частное уже на своих местах. Если счетчик еще не нулевой, то возвращаемся к шагу 2.
Наконец, текст программы.
;
; Секция данных процедуры деления.
;
div_dat udata_shr
dividend res 1 ; делимое, один байт
divider res 1 ; делитель, один байт
quotient res 1 ; частное, один байт
remainder res 1 ; остаток, один байт
counter res 1 ; счетчик сдвигов/вычитаний
;
; Секция кода процедуры деления.
;
Division code
Udiv8x8:
; Шаг 1, инициализация счетчика
movlw .8
movwf counter ; Всегда обрабатываем все биты
; Шаг 2, перенос очередного разряда делимого в остаток
Step2:
rlf dividend,f
rlf remainder,f
; Шаг 3, вычитание и определение значения очередного разряда частного
movf divider,w
subwf remainder,w
btfss STATUS,C
goto Negate
rlf quotient,f
movwf remainder
goto Step4
Negate:
rlf quotient,f
; Шаг 4, проверка завершения деления
Step4:
decfsz counter,f
goto Step2
return
В памяти данных занято по прежнему 5 байт. А вот сама процедура занимает только 15 слов. В два раза меньше! Посмотрим на быстродействие. Первый шаг всегда выполняется за 2 машинных цикла. На каждую итерацию цикла потребуется 11 или 13 машинных циклов. И два цикла на команду возврата. В худшем случае все потребуется 108 циклов, а в лучшем 92. А что насчет обработки ошибок? Если делитель равен нулю, то получим частное 255 и остаток равный делителю, что и позволит сделать вывод об ошибке.
Небольшой промежуточный итог
Можно подвести итоги. Второй вариант алгоритма занимает в два раза меньше места в памяти программ и быстрее первого в худшем случае. Зато гораздо медленнее в лучшем случае. В среднем, первый вариант алгоритма потребует порядка 80 машинных цикла, а второй около 100. Какой вариант лучше? Решать вам. Если критично занимаемое кодом место, то однозначно второй. А вот выбор по быстродействию не так прост и сильно зависит от обрабатываемых чисел. Большей частью от делителя. При критичности быстродействия имеет смысл попробовать оба варианта в реальных ситуациях и выбрать лучший.
А теперь, как и обещал, я вас распутаю. На самом деле эти два варианта абсолютно одинаково выполняют само деление. Сам цикл деления (шаги с 3 по 5) в первом варианте занимает 15 команд, как и во втором варианте. Оставшиеся 14 команд это проверка делителя на 0, обработка ошибки и нормализация. Только в первом варианте основной цикл выполняется от 1 до 8 раз, а во втором варианте всегда 8.
Еще раз посмотрите на деление в столбик. В каждой итерации цикла деления у нас участвует только часть разрядов делимого и все разряды делителя. Для упрощения вычитания делитель не должен пересекать границы байта, в нашем, 8-разрядном, случае. Но начинать мы все равно должны со старших разрядов делимого. В первом варианте мы обеспечиваем оба эти условия шагом нормализации, которая обеспечивает и меньшее количество итераций цикла, но сама требует время на выполнение. Во втором варианте мы переносим обрабатываемые разряды делимого в отдельный байт, из которого и вычитаем делитель. При этом нам всегда надо обрабатывать все разряды.
Так что алгоритм деления один, различаются только детали его реализации. Причем эти детали зависят от архитектуры процессора, в нашем случае, микроконтроллера. Например, в Extended MidRange PIC (не PIC18) есть команды сложения и вычитания с учетом переноса и арифметические сдвиги. А в PIC18 команды проверки условия и двухадресная команда пересылки. Поэтому различие двух вариантов реализации может быть как очень сильным, так и совсем незначительным.
В первом приближении можно считать первый вариант реализации попыткой оптимизации времени выполнения за счет увеличения длины программы. А второй вариант оптимизацией по размеру за счет увеличения времени выполнения.
А что она счет большей разрядности?
Я не ставлю целью статьи описание всех возможных ситуаций. Да и готовой универсальной библиотеки не будет. Но, пожалуй, затрону вопрос деления 16-разрядного числа на 8 разрядное. Необходимость в этом встречается не так редко. Но буду рассматривать только второй вариант реализации алгоритма, то есть, со сдвигом делимого.
Сначала отмечу особенности результатов деления. Частное может занимать столько же разрядов, сколько делимое. Действительно, если мы делим на единицу, то частное будет равно делимому. А вот остаток всегда меньше делителя. Значит, частное у нас тоже будет 16-разрядным, как и делимое. Остаток будет 8-разрядным, как и делитель.
На первый взгляд, изменения в программе будут минимальны. Достаточно в счетчик загрузить 16, на втором шаге сдвигать не два, а три байта, сдвиг частного будет затрагивать два байта. И все должно заработать. Но давайте посмотрим, что может быть когда все 8 разрядов делителя являются значащими. То есть, старший разряд делителя равен единице (делитель больше 128, 10000000 в двоичном виде). А может возникнуть ситуация, когда на очередной итерации цикла текущее значение остатка будет тоже содержать единицу в старшем разряде, но разность окажется отрицательной. Например, текущее значение остатка 10110011, а делитель 11001100. Это не страшно, если мы уже обработали все разряды (счетчик обнулился), тогда текущее значение остатка просто будет остатком от деления. Но если деление еще не закончено, то на следующей итерации у нас текущий остаток выйдет за границы байта, что недопустимо. При 8-разрядном делимом такого произойти не могло. Подумайте почему. Придется учитывать эту тонкость. На сам алгоритм это не повлияет, но шаг 3 немного усложнится. А теперь получившаяся программа
;
; Секция данных процедуры деления.
;
div_dat udata_shr
dividend res 2 ; делимое, два байта
; старший байт делимого будет
; находиться по адресу
; dividend+1
divider res 1 ; делитель, один байт
quotient res 2 ; частное, два байта
remainder res 1 ; остаток, один байт
counter res 1 ; счетчик сдвигов/вычитаний
;
; Секция кода процедуры деления.
;
Division code
Udiv16x8:
; Шаг 1, инициализация счетчика
movlw .16
movwf counter ; Всегда обрабатываем все биты
; Шаг 2, перенос очередного разряда делимого в остаток
Step2:
rlf dividend,f
rlf dividend+1,f
rlf remainder,f
; Шаг 3, вычитание и определение значения очередного разряда частного
; *** в этом месте флаг переноса у нас 1, если текущий остаток вышел
; за границы байта. Этот случай мы должны обрабатывать отдельно
btfsc STATUS,C
goto Step3a ; на обработку особого случая
movf divider,w
subwf remainder,w
btfss STATUS,C
goto Negate
rlf quotient,f
rlf quotient+1,f
movwf remainder
goto Step4
Step3a:
movf divider,w
subwf remainder,f ; разность всегда положительна
bsf STATUS,C
Negate:
rlf quotient,f
rlf quotient+1,f
; Шаг 4, проверка завершения деления
Step4:
decfsz counter,f
goto Step2
return
На шаге 3 появилась проверка выхода остатка за границу байта, это можно определить по состоянию флага переноса, куда выдвигается старший разряд. А обработка этого случая выполняется на шаге 3а. Не смотря на то, что операция вычитания не учитывает выход уменьшаемого (остатка) за границу байта, ее результат будет правильным в пределах байта. Можете проверить сами. А вот знак разности будет ошибочным, что мы и исправляем принудительной установкой флага переноса. Размер программы увеличился незначительно. Увеличился и занимаемый размер памяти данных, что естественно.
Программы можно немного оптимизировать по размеру не увеличивая время выполнения. Например, можно заметить, что сдвиги частного выполняются в двух местах (для двух случаев), при этом они совершенно идентичны. Можно оставить сдвиг только в одном месте, если учесть, что команда movwf не изменяет состояние флага переноса. Попробуйте сделать эту оптимизацию самостоятельно, я не стал ее делать для сохранения большей наглядности. Но в программе деления 16-разрядного числа на 8-разрядное такая оптимизация частично есть (иначе сдвиг частного был бы трех местах).
А как быть с числами со знаком?
Числа со знаком, обычно, обрабатывают как числа без знака. При этом для отрицательных значений меняется знак (берется модуль числа). Как сменить знак числа, если немного забыли, можно почитать в упоминавшейся в начале статье о простых типах данных. Частное от деления знаковых чисел будет положительно, если делимое и делитель имеют одинаковые знаки. Иначе, частное будет отрицательно, то есть, ему придется еще раз сменить знак после деления (мы же делили числа без знака, то есть, положительные). Остаток всегда будет иметь знак делимого. И для отрицательного делимого знак остатка тоже придется подкорректировать.
Заключение
Деление считается самой сложной операцией из четырех арифметических. И в виде готовой команды микроконтроллера оно встречается реже всего. Но программная реализация оказалась вовсе не такой страшной, хотя и очень медленной по сравнению с аппаратно реализованными командами. Для деления на известные на этапе написания программы константы лучше использовать комбинации сдвигов/вычитаний/сложений. Увеличение разрядности делимого не вызывает особых проблем и не ведет к резкому увеличению размера программ. Увеличение разрядности делителя гораздо серьезнее, но непреодолимых трудностей тоже нет. Если же требуется делить числа с разрядностью многократно превышающей разрядность микроконтроллера, то действительно имеет смысл задуматься о его замене на более подходящий.
Отмечу преимущество нашей реализации деления перед операцией деления в языках высокого уровня - мы сразу получаем и частное, и остаток. Да, в stdlib есть функция div, которая тоже позволяет получить и частное, и остаток (структура div_t). Но, во первых, не во всех компиляторах эта библиотека доступна. Во вторых, посмотрите на такую шедевральную, иначе и не скажешь реализацию функции div в одном из компиляторов для 8-разрядных микроконтроллеров PIC
div_t div(signed int numer, signed int denom) {
div_t val;
val.quot = numer / denom;
val.rem = numer - (denom * val.quot);
return (val);
}
В 8 разрядных PIC команды деления нет, значит оно выполняется только программно. Как мы видели, при этом получается и частное, и остаток. Но в этой реализации остаток предпочитают получать еще раз, причем через умножение! Замечу, что команда умножения есть не во всех 8 разрядных PIC. Я не буду называть компилятор и его производителя. Но замечу, что это коммерческий компилятор, и совсем не дешевый. Поэтому, знать описанные в этой статье алгоритмы деления может быть полезно даже в том случае, если Вы используете другие контроллеры и всегда пишете программы только на языках высокого уровня.
Вы можете обсудить данную статью или задать вопросы автору на форуме